Nvic 1-15 - Fill online, Printable, Fillable Blank

👉

Did you like how we did? Rate your experience!

Rated 4.5 out of 5 stars by our customers

Award-winning PDF software

review-platform

review-platform

review-platform

review-platform

review-platform

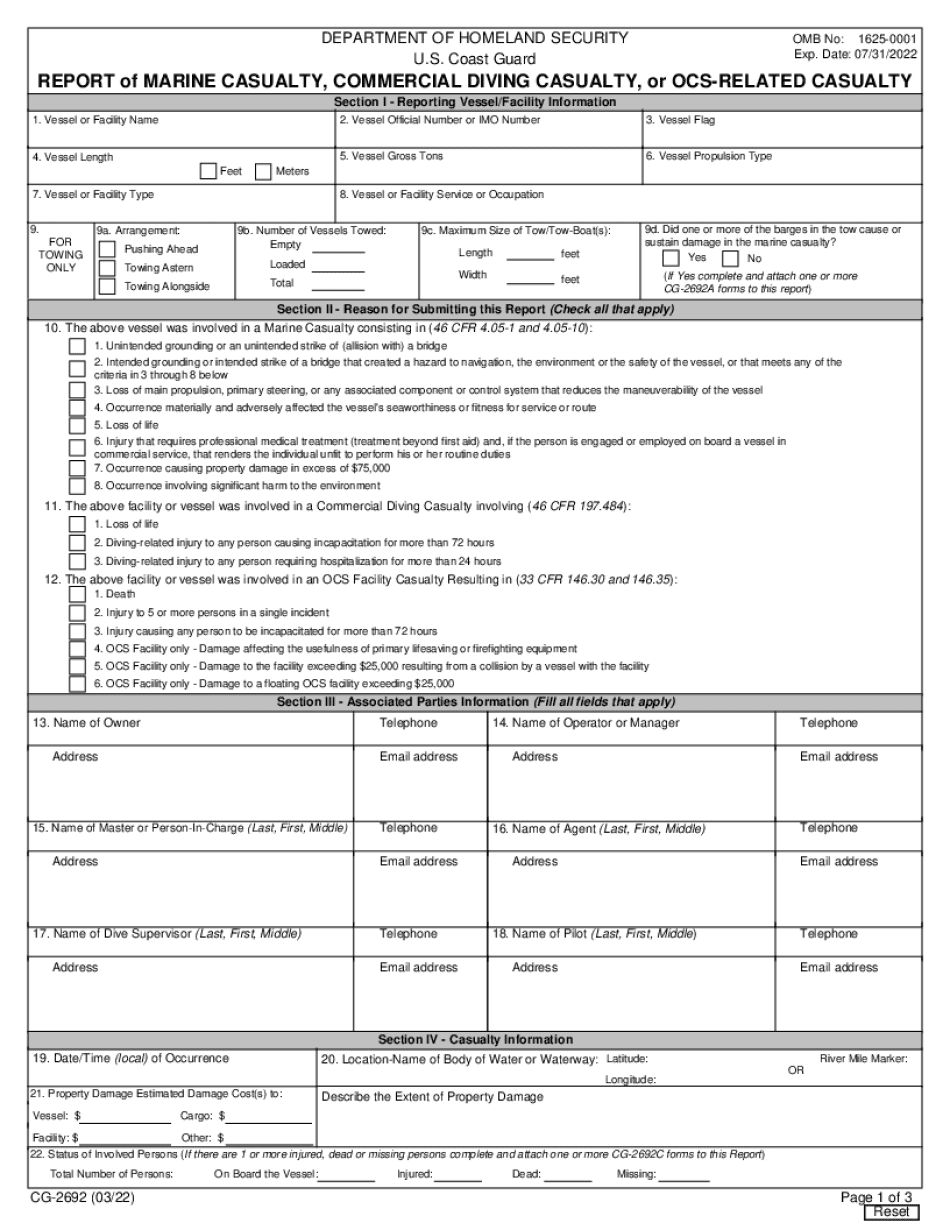
Nvic 1-15 Form: What You Should Know

Addendum The new version of the navigation and vessel inspection circular, “Navigation and Vessel Inspection Circular-VIC 01-15,” is effective for all personnel of the Coast Guard who report marine casualty information to: — Coast Guard Search and Rescue (STAR); U.S. Coast Guard Reserve personnel. -- Marine Corps Region-X (RX): The Commandant of the Coast Guard. As required elsewhere in the Navy/circular, each individual marine casualty need only describe—in the “Contact Us” section—the event to which they are referring. A Marine casualty reports the information as either: “Marine Casualty Name” or “Contact Name.” “Contact Name” is required for all marine casualties.

Online solutions help you to manage your record administration along with raise the efficiency of the workflows. Stick to the fast guide to do CG-2692 Form, steer clear of blunders along with furnish it in a timely manner:

How to complete any CG-2692 Form online:

On the site with all the document, click on Begin immediately along with complete for the editor.
Use your indications to submit established track record areas.
Add your own info and speak to data.
Make sure that you enter correct details and numbers throughout suitable areas.
Very carefully confirm the content of the form as well as grammar along with punctuational.
Navigate to Support area when you have questions or perhaps handle our assistance team.
Place an electronic digital unique in your CG-2692 Form by using Sign Device.
After the form is fully gone, media Completed.
Deliver the particular prepared document by way of electronic mail or facsimile, art print it out or perhaps reduce the gadget.

PDF editor permits you to help make changes to your CG-2692 Form from the internet connected gadget, personalize it based on your requirements, indicator this in electronic format and also disperse differently.

FAQ - Nvic 1-15

Can you add 5 odd numbers to get 30?

It is 7,9 + 9,1 + 1 + 3 + 9 = 30Wish you can find the 7,9 and 9,1 in the list of1,3,5,u00a0u00a0 7,9u00a0u00a0u00a0 ,11,13,151,3,5,7,u00a0u00a0u00a0u00a0u00a0 9,1u00a0u00a0u00a0 1,13,15

How do I fill out the educational qualification section of the assistant commandant application form in coast guard (01/2024 batch)?

U should be Bachelor of science hieght166 wt 50 and pass ur exams

How many colleges I can fill out as choices for the All India 15% Quota?

There isnu2019t any limit as to how many choices you can fill in during the counseling. In the end remember to put those choices at the top which you prefer over others. Seats are allotted based on your preference so choose wisely.

Mathematical Puzzles: What is + + = 30 using 1,3,5,7,9,11,13,15?

My question had been merged with another one and as a result, I have added the previous answer to the present one. Hopefully this provides a clearer explanation. Just using the numbers given there, it's not possible, because odd + odd = even, even + odd = odd. 30 is an even number, the answer of 3 odd numbers must be odd, it's a contradiction. If what people say is true, then the question is wrongly phrased its any number of operations within those three brackets must lead to 30. Then it becomes a lot easier. Such as 15 + 7 + (7 + 1). That would give 30. But it assumes something that the question does not state explicitly and cannot be done that way. I still stick to my first point, it can't be done within the realm of math and just using three numbers, if not, then the latter is a way to solve it.EDIT:u00a0u00a0 This question has come up many times, Any odd number can be expressed as the following, Let [math]n, m, p[/math] be an odd number, [math] n = 1 (mod[/math] [math]2), m = 1 (mod[/math] [math]2), p = 1 (mod[/math] [math]2)[/math][math]n+m+p = 1 + 1 + 1 (mod[/math] [math]2)[/math]Let's call [math]n+m+p[/math] as [math]x[/math][math]= x = 3 (mod[/math] [math]2)[/math]Numbers in modulo n can be added, I'll write a small proof for it below, [math]a = b (mod[/math] [math]n), c = d (mod[/math] [math]n)[/math][math]a+c = b+d (mod[/math] [math]n)[/math]We can rewrite [math]b[/math] and [math]d[/math] in the following way, [math]n | (b - a) = b-a = n*p[/math] (for some integer p) [math]b = a + np[/math][math]b = a + np, d = c + nq[/math][math]b + d = a + np + c + nq[/math][math]b+d = a + c + n(p + q)[/math]Now we have shown that our result is true, moving forward, [math]3 = 1 (mod[/math] [math]2)[/math][math]x = 1 (mod[/math] [math]2)[/math]Therefore the sum of three odd numbers can never be even. It will always be congruent to 1 in mod 2.(This was what I wrote for a merged answer).Modular arithmeticu00a0 - Link on modular arithmetic, the basic operations. Modular multiplicative inverse - The multiplicative inverse in modular operations.Congruence relationFermat's little theorem Modular exponentiation - As title suggests.Good luck!

How do I get my TDS back if I forgot to fill out my 15H?

simpleu2026file your incometax and claim the deducted TDS (if salary is within no-tax criteria)

If you believe that this page should be taken down, please follow our DMCA take down process here.

Loading, please wait...